Beregning af Gini-koefficient

 ​

Data til beregning af gini-koefficienten kan findes flere steder. Et oplagt sted er statistikbanken.dk under indkomster, fx INDKP105 (indkomst før skat) eller INDKP106 (disponibel indkomst). Data for USA kan findes her: Indkomstfordeling for husstande i USA fra 1967 til 2015.

 ​

De valgte data bør tilpasses så de ligner de nedenstående data. Der skal være indkomstintervaller opgjort i antal personer i gruppen og det samlede indkomstbeløb i gruppen.

Man starter med at finde summen af både antal personer og indkomstbeløb.

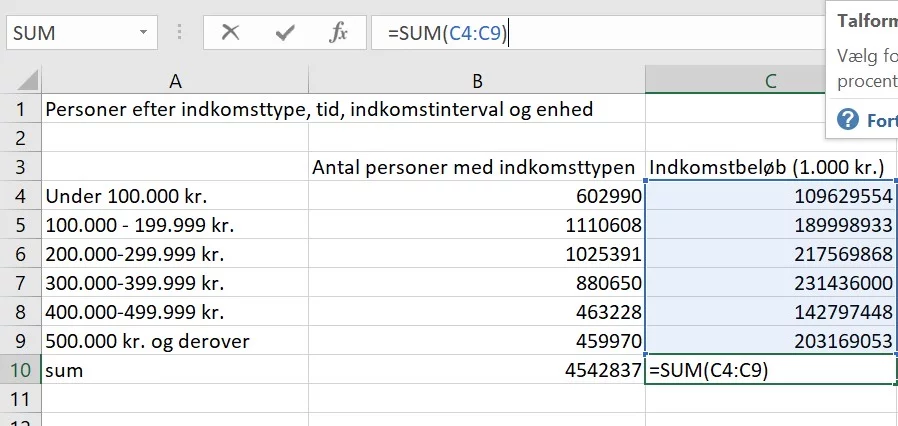
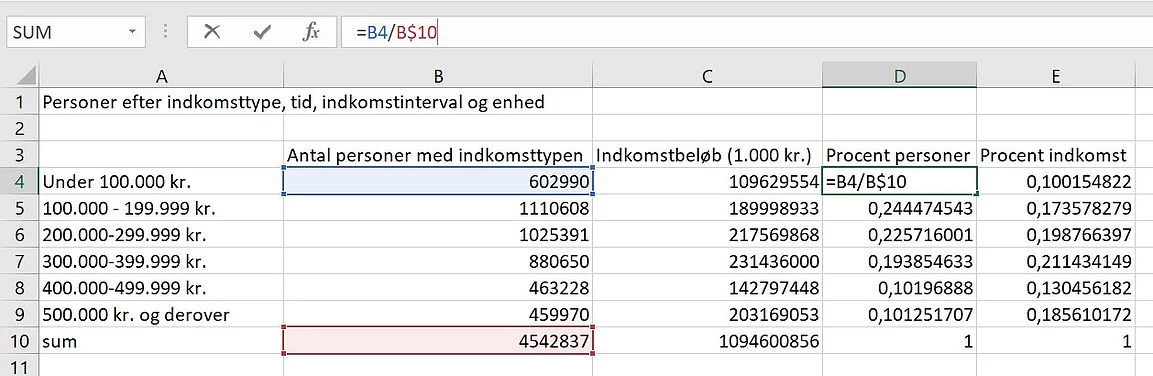
Herefter beregnes procentandelen (dog som decimalbrøk) af hvert datapunkt i forhold til den tidligere beregnede sum. Vi bruger dollartegn ($) til at låse vores sum-række så den ikke ændres når vi kopierer formelen. Formelen for procentandelen af antal personer i indkomstintervallet under 100.000 kr., i forhold til det samlede antal personer, bliver: =B4/B$10 Den kopieres til alle felter under procent personer og procent indkomst.

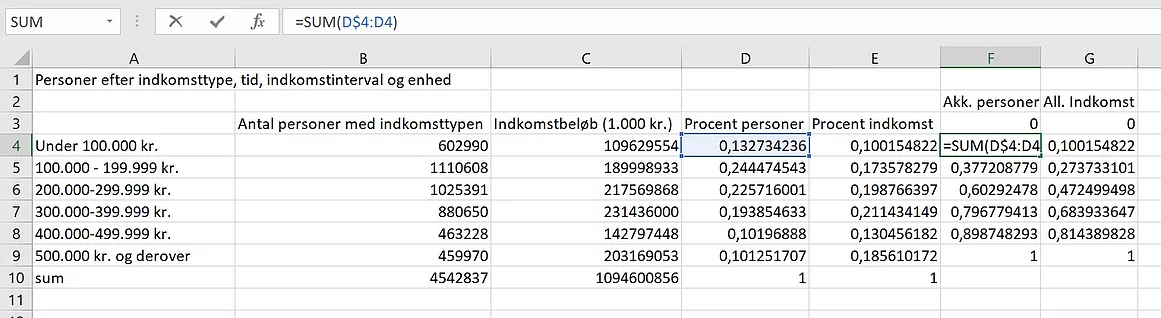
Så beregnes de akkumulerede procenter af både personer og indkomster. Formålet med dette er at få koordinater til at tegne en Lorenz-kurve i et koordinatsystem. Vælg feltet i den laveste indkomst kategori (her under 100.000 kr.) og akkumulerede personer og indtast følgende formel: =SUM(D$4:D4) og kopier den til alle felter under akkumulerede personer og indkomster. Bemærk dollartegnet ($), der låser rækken med den laveste indkomst kategori (her under 100.000 kr.).

Derudover indsættes øverst et nul under akkumulerede personer og indkomster. Så har vi koordinaterne til vores Lorenz-kurve.

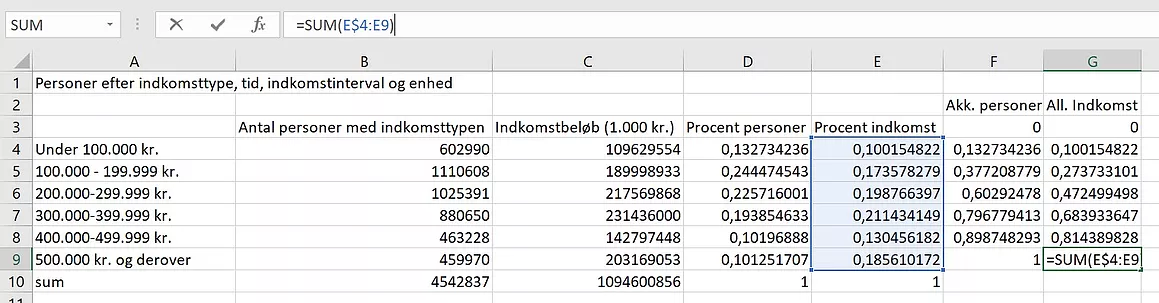
Marker alle felterne med de koordinater vi skal bruge.

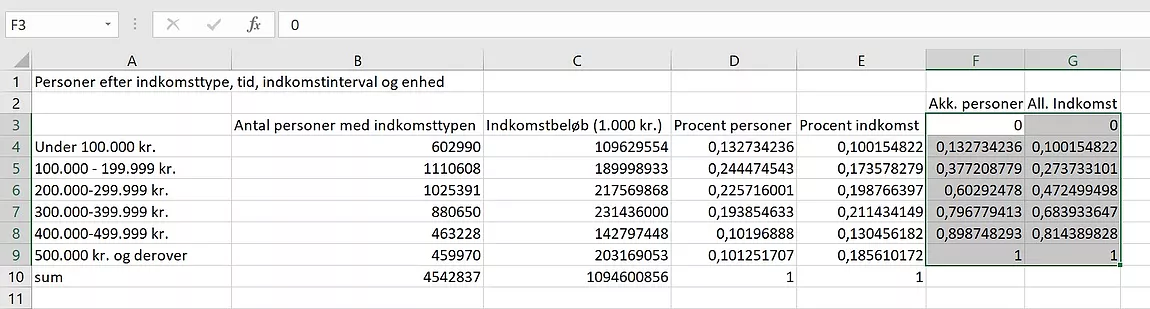
Og indsæt et punktdiagram.

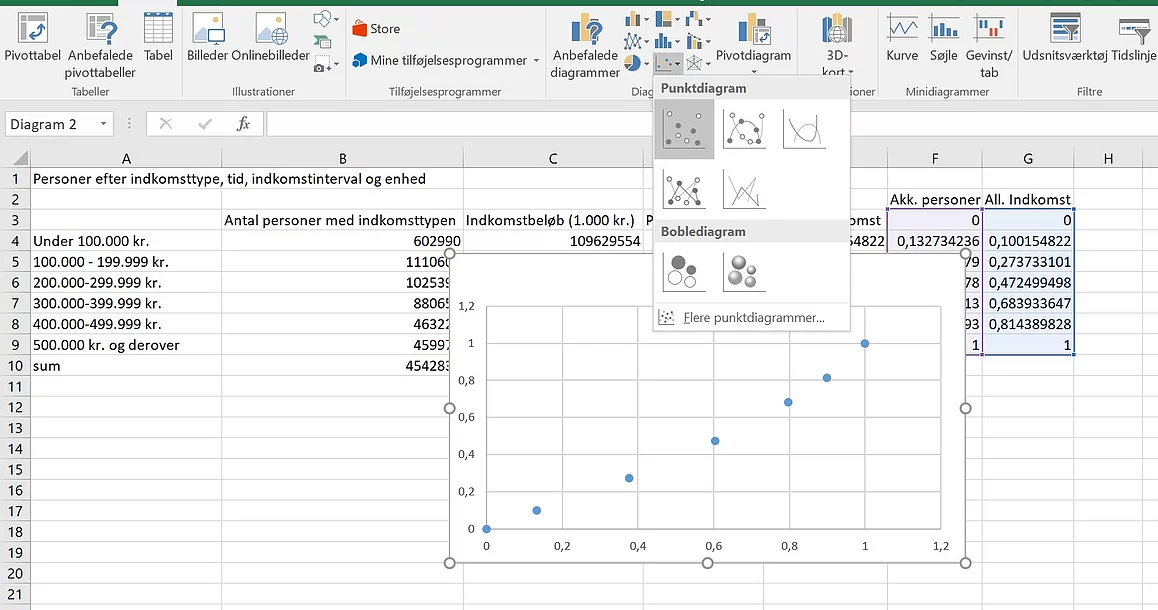
Tilføj en tendenslinje til punktdiagrammet.

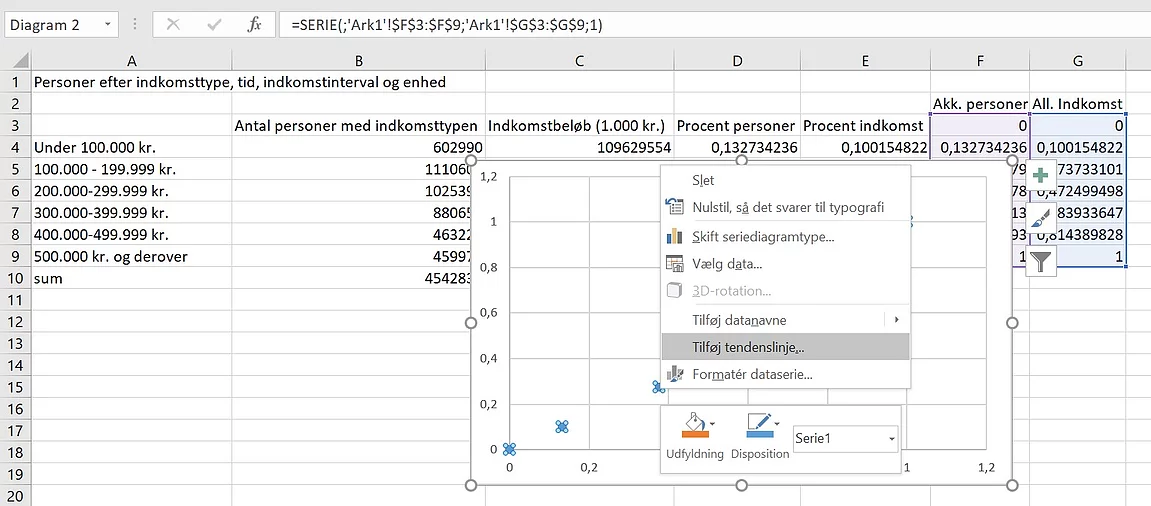
Vælg polynomisk og vælg hvilken grad polynomiet skal have. Brug gerne 2, som er standard. Dvs. en andengradsligning.

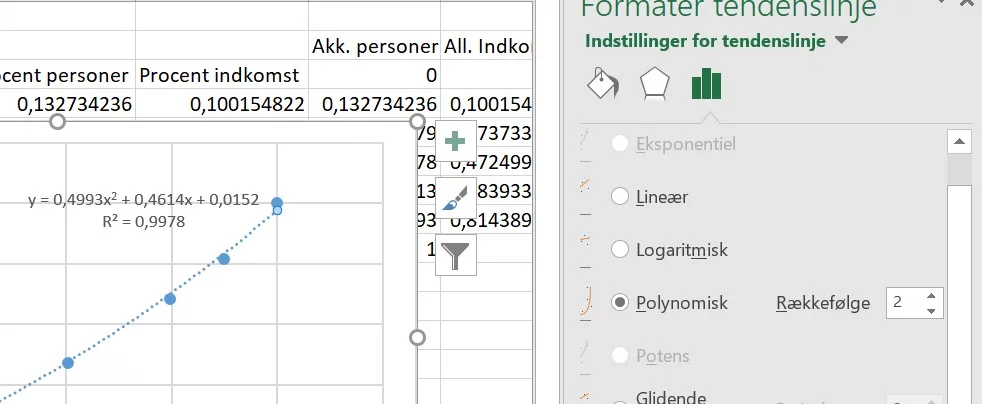
Vælg Vis ligning i diagram og vælg Vis R-kvadreret værdi i diagram.

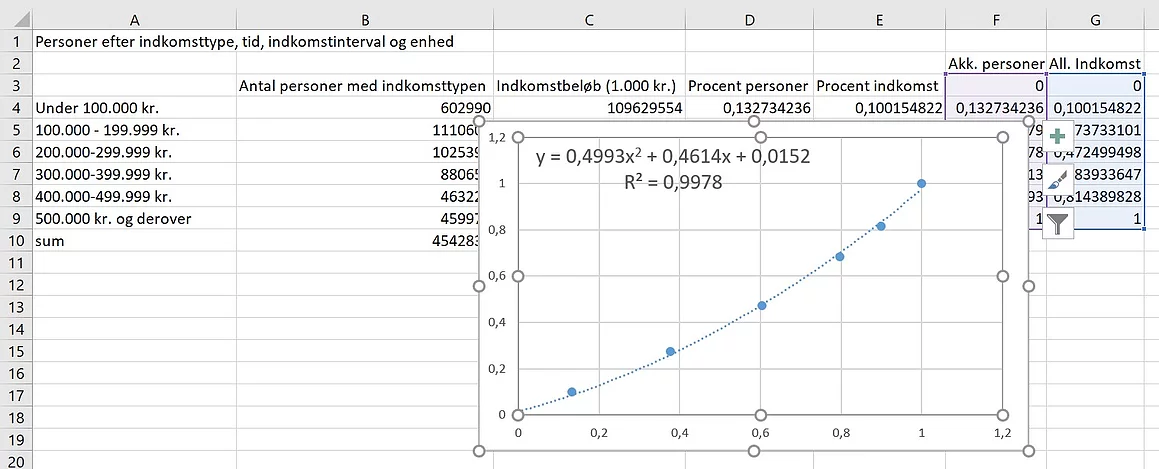
Så har du en Lorenz-kurve over dine data. Din R2-værdi, fortæller hvor godt den passer med dine punkter og din ligning skal du bruge til at beregne Gini-koefficienten.

 

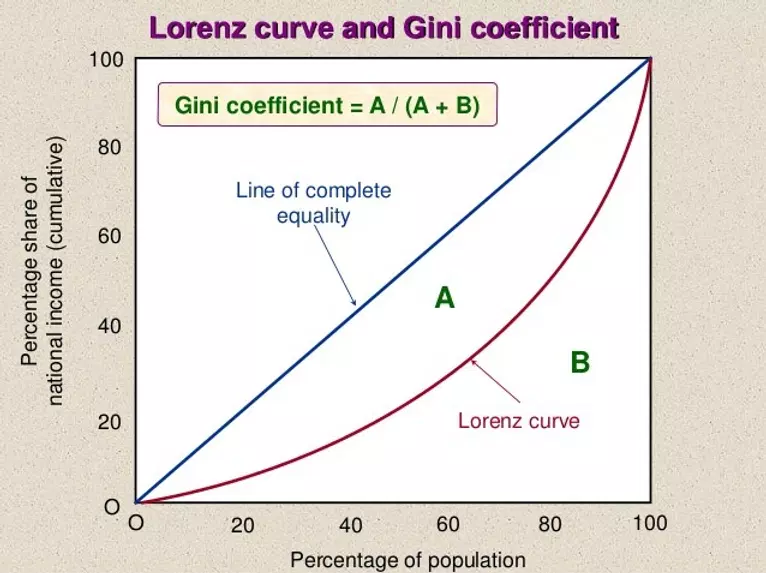
På nedenstående figur kan du se hvordan Gini-koefficienten er defineret. A er arealet mellem din Lorenz-kurve og en 45-graders vinkel linje, der angiver fuldstændig lighed, og skærer dit koordinatsystem i to dele. B angiver arealet under Lorenz-kurven. Gini-koefficienten er lig med A/(A+B). Dvs. A som en andel af A+B.

Vi ved at A+B=½ fordi A+B udgør en trekant, der udgør halvdelen af et kvadrat på 1x1.

 ​

Da Gini-koefficienten er defineret som A/(A+B) kan vi udlede at:

  

A+B=½

 Gini=A/(1/2)=2A  

 A=½-B

 Gini=2(½-B)=1-2B

 ​

Dermed kan vi beregne Gini-koefficienten ved at beregne B og indsætte den I formelen: 1-2B

 

Vi beregner B ved at beregne integralet for Lorenz-kurven fra 0 til 1. Vi bruger formelen for vores Lorenz-kurve, som vi fandt før. y = 0,4993x2 + 0,4614x + 0,0152

 

 

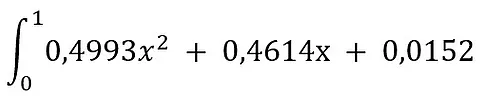
Dette kan fx beregnes vha. følgende webside: https://www.symbolab.com/solver/definite-integral-calculator

 ​

Husk at ændre formel så den passer til websiden, bl.a. med engelsk komma.

​

​Resultatet giver at B=0,41233 og dette indsættes i Gini=1-2B, som giver 0,17534. Vores Gini-koefficient er dermed, ud fra de brugte data, ca. 0,175.