Chi²-test guide

Dette er en kort guide til at lave chi²-test i Excel. Denne guide undersøger om køn påvirker partivalg. Et link til en mere detaljeret matematisk forklaring kan findes i slutningen af denne guide. Det er meningen at denne guide kun beskriver hvordan en test kan laves i Excel.

Vi starter med at formulere vores nulhypotese og alternative hypotese. Vores P-værdi og signifikansniveau fortæller os så om vi accepterer den ene eller den anden hypotese. Se senere for en matematisk forklaring af hvorfor vi gør dette.

Køn er uafhængig variabel og partivalg er afhængig variabel. Dvs. partivalg afhænger af køn, men ikke omvendt.

Nulhypotese: Køn påvirker ikke partivalg

Alternativ hypotese: Køn påvirker partivalg

Man starter med sine observerede data.

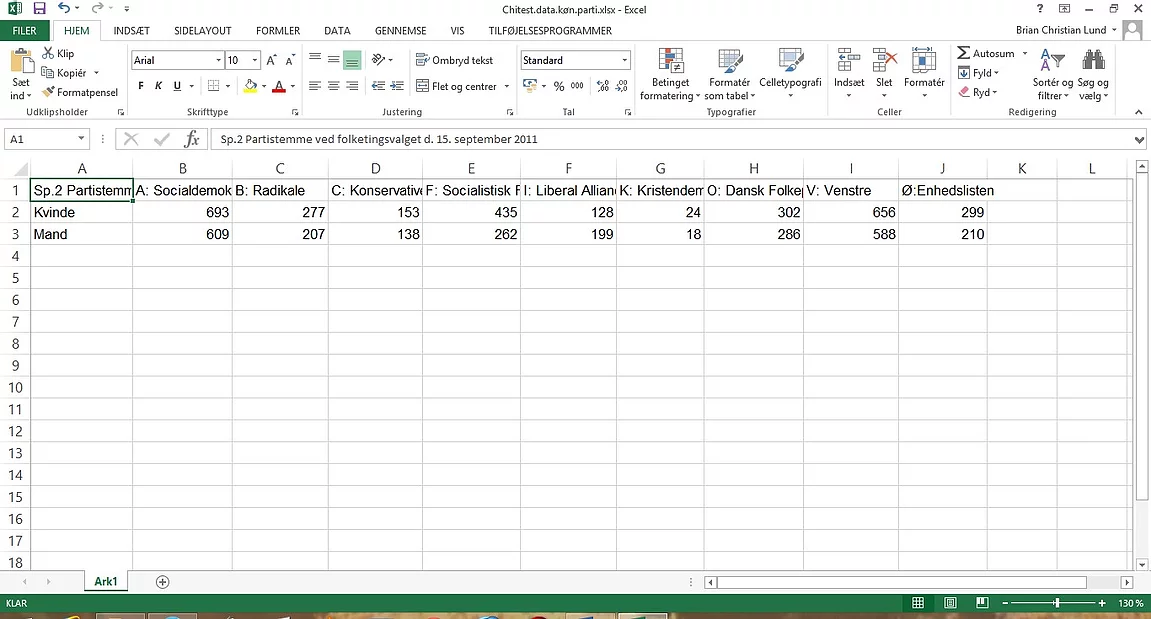
Det første man gør er at lave summer for alle rækker og kolonner. Det gøres med kommandoen =SUM(B2:J2), hvor tallene fra B2 til J2 lægges sammen.

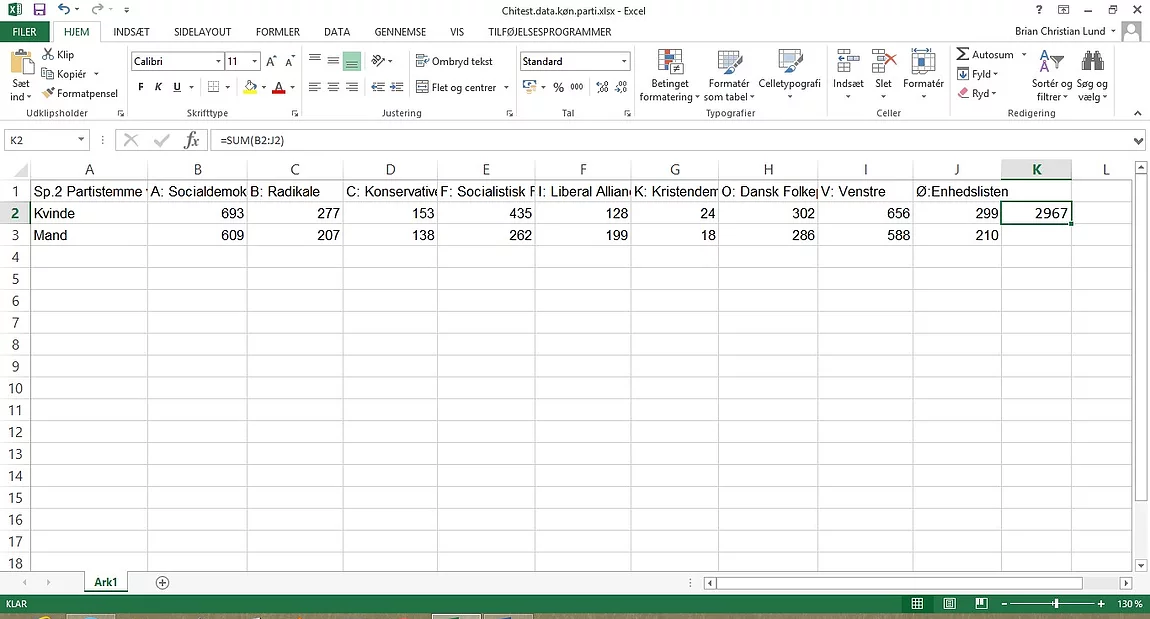
Feltet med beregningen kan kopieres til række 3 så man ikke behøver skrive kommandoen igen. Brug fx ctrl+c og ctrl+v til kopiering eller du kan trække i den lille firkant i nederste højre hjørne af feltet. Det samme kan gøres med kolonnerne.

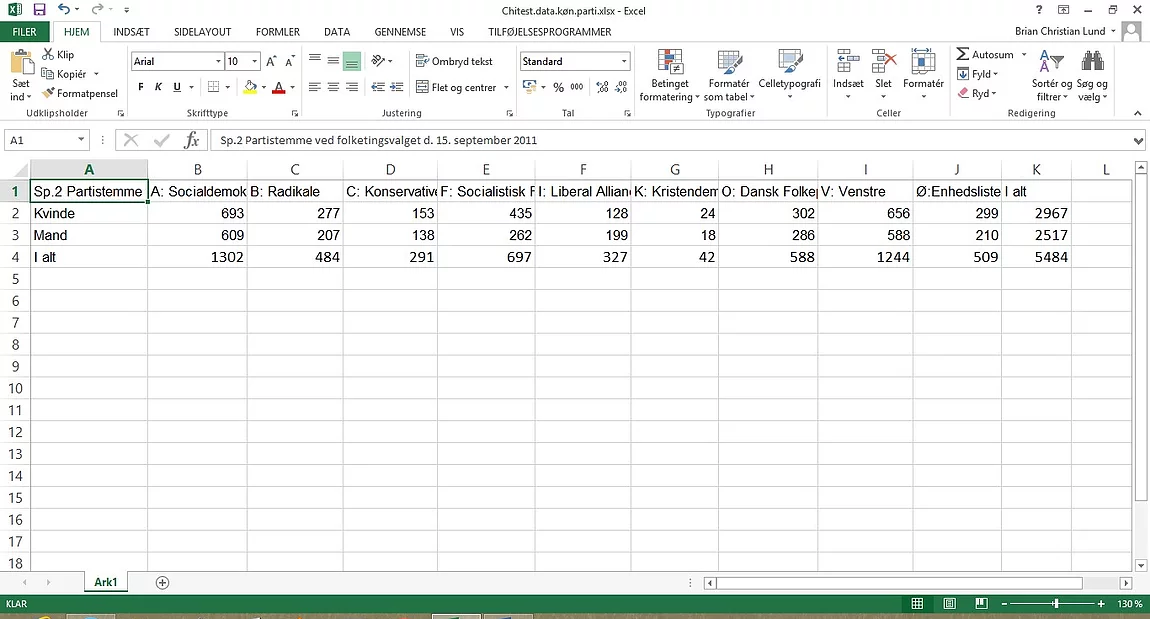
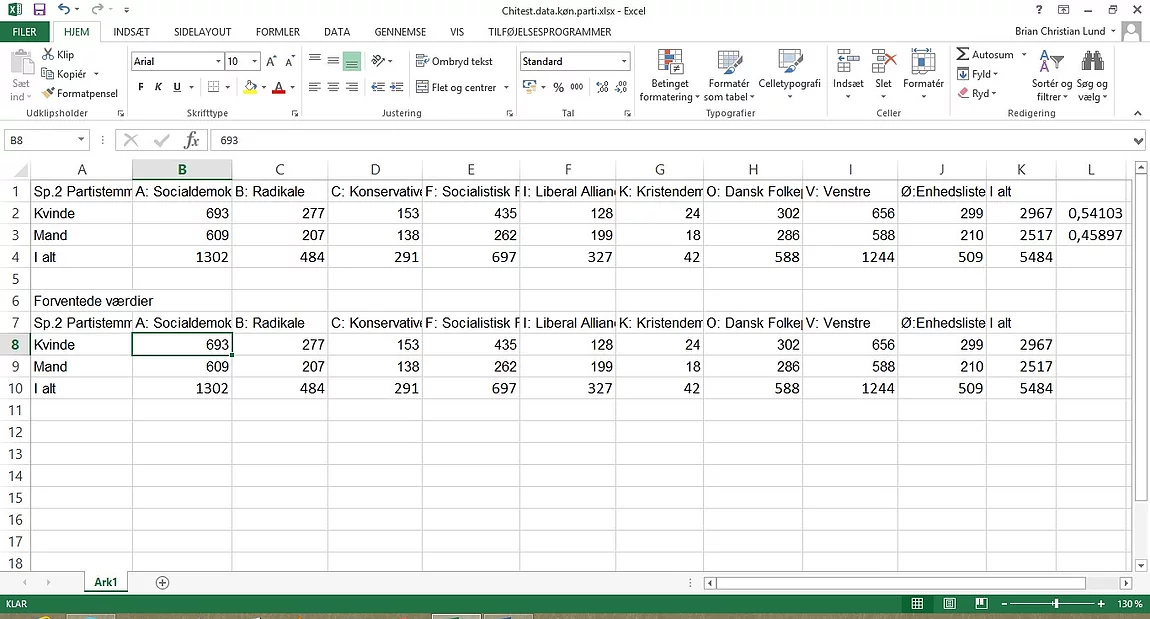
Det næste vi skal beregne er fordelingen af mænd og kvinder i undersøgelsen. Det skal vi gøre med vores kolonne K – I alt. Vi bruger kommandoen: =K2/K$4 i L2 og kopierer den til L3. Bemærk dollartegnet ($). Dollartegnet foran 4-tallet gør at 4-tallet ikke ændres når vi kopierer vores formel. Det er vigtigt fordi vi skal beholde række 4 – I alt – som vores nævner i vores beregning. Resultatet ser sådan ud:

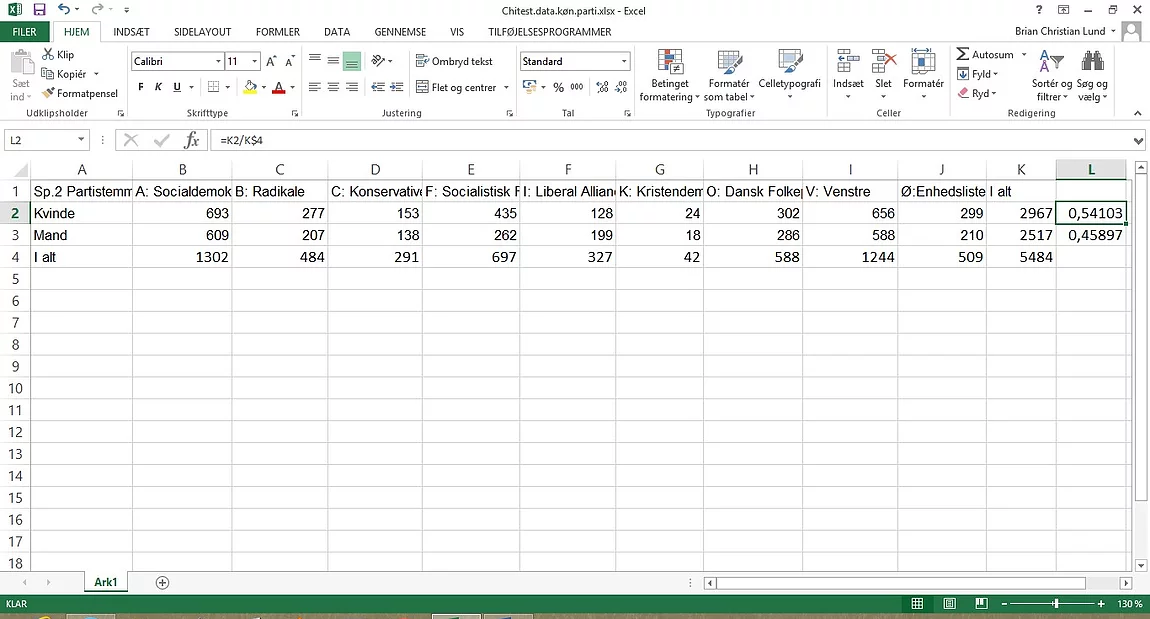
Vi kan se at der er ca. 54% kvinder og ca. 46% mænd i undersøgelsen.

Forventede værdier:

Vi skal nu beregne vores forventede værdier. Vi starter med at kopiere hele vores tabel med observerede værdier, inkl. I alt, til lidt længere nede i regnearket.

De forventede værdier er de værdier vi ville forvente, hvis der ingen sammenhæng mellem køn og partivalg er. Det betyder at vi ville forvente at fordelingen af mænd og kvinder, blandt vælgerne hos de enkelte partier, er den samme som fordelingen af mænd og kvinder hos alle der deltager i undersøgelsen.

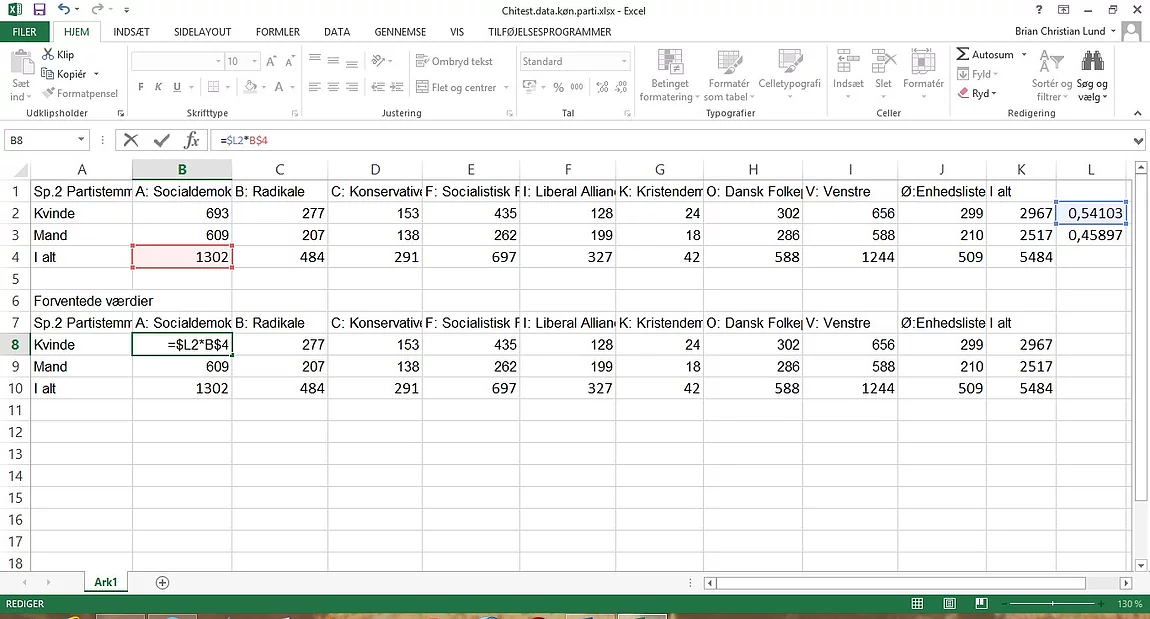
Dette gør vi ved at gange vores beregnede kønsfordeling ind i vores i alt for hvert parti. Vi starter med socialdemokratiet. Dette kan ses i billedet nedenfor. Vi bruger dollartegn for at låse vores række 4 og søjle L, da det er denne række og søjle der bruges for begge køn og alle partier. Det forventede antal kvinder, i undersøgelsen, der stemmer på Socialdemokratiet, beregnes derfor med: =$L2*B$4

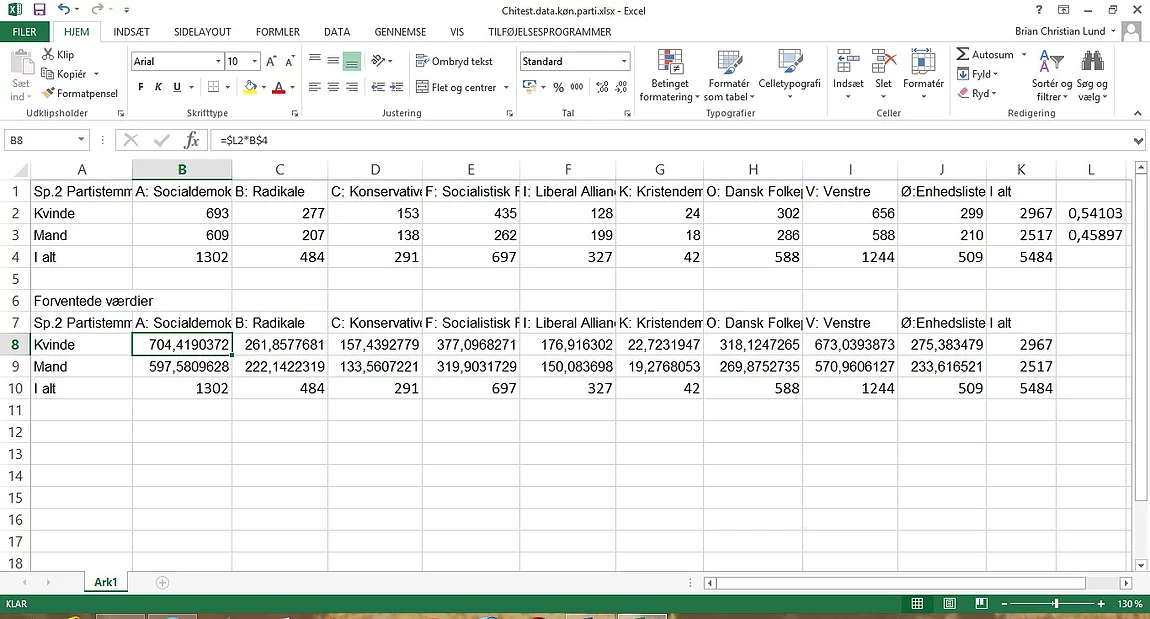
Denne formel kopieres til alle den forventede tabels søjler og vi får det nedenstående resultat. Vi kan se at summerne er ens i både vores observerede og forventede værdier og dermed har vi beregnet korrekt.

Beregning af P-værdi:

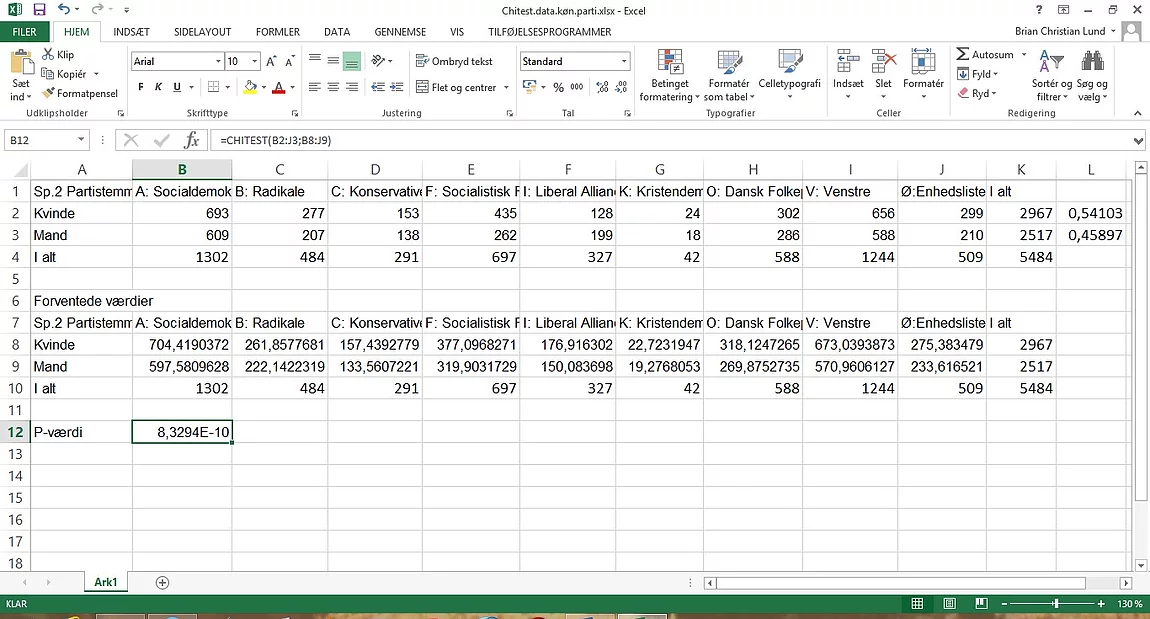
Det sidste vi gør er at beregne vores P-værdi. Vi bruger den kommando i Excel, der hedder CHITEST. Vi finder en ledig celle. Vi skriver =CHITEST( og vælger derefter alle de observerede værdier (uden summer). Vi adskiller med et semikolon (;). Vi vælger de forventede værdier (igen uden summer) og afslutter med en parentes ). Vores kommando ser sådan ud: =CHITEST(B2:J3;B8:J9)

Nedenfor kan resultatet ses.

Fortolkning af P-værdien:

P-værdien er resultatet af en chi-i-anden test. P-værdien er et tal mellem 0 og 1. P-værdien bør være under 0,05.

P-værdien angiver, hvor stor sandsynligheden er for at en ny stikprøve (vores indsamlede data) vil være mindre repræsentativ for populationen (den gruppe vi undersøger) end den stikprøve vi laver chi-i-anden test på. Hvis den ikke er repræsentativ kan vi ikke bruge stikprøven til at lave konklusioner for populationen. Jo lavere P-værdien er jo mindre er sandsynligheden for at vores data ikke er repræsentative.

Den typisk acceptable grænse, også kaldet signifikansniveauet, for P-værdien er 0,05. Dvs. P-værdien skal være under 0,05 for at vi kan konkludere noget ud fra vores datasammenhæng. Bemærk dog at denne værdi ikke er magisk. Det er værd at overveje om vi stadig kan bruge vores data selv hvis P-værdien er 0,07. Grundlæggende drejer det sig om hvor risikovillige vi er. Jo mere risikovillige vi er jo højere P-værdi kan vi acceptere. Men normal standard er at P-værdien bør være under 0,05.

Yderligere hjælp til chi-i-anden test

Se her for en matematisk forklaring på chi-i-anden testen:

http://www.webmatematik.dk/lektioner/matematik-b/statistik/chi-i-anden-test